「速さ、時間、距離」の計算、なんだか難しそう…と苦手意識を持っていませんか?「はじき計算(みはじ計算とも言います)」は、その関係性を一つの図でカンタンに覚えられる便利な方法です。
この記事では、「はじき計算」の基本的な使い方から、文章問題でつまずかないためのコツまで、わかりやすく解説していきます。この記事を読み終える頃には、「速さ・時間・距離」の問題が得意になっているはずですよ。
「はじき計算」とは?まずは基本の図を覚えよう
「はじき計算」とは、「は(速さ)」「じ(時間)」「き(距離)」の3つの関係性を覚えるための方法です。
(「みはじ」の場合は、「み(道のり)」「は(速さ)」「じ(時間)」となります。意味はまったく同じです)
この計算が活躍するのは、主に小学校の算数ですが、中学・高校の数学や物理でも基本となる、とっても大事な考え方なんです。
多くの場合、テントウムシのイラストや円を使った図で習いますよね。
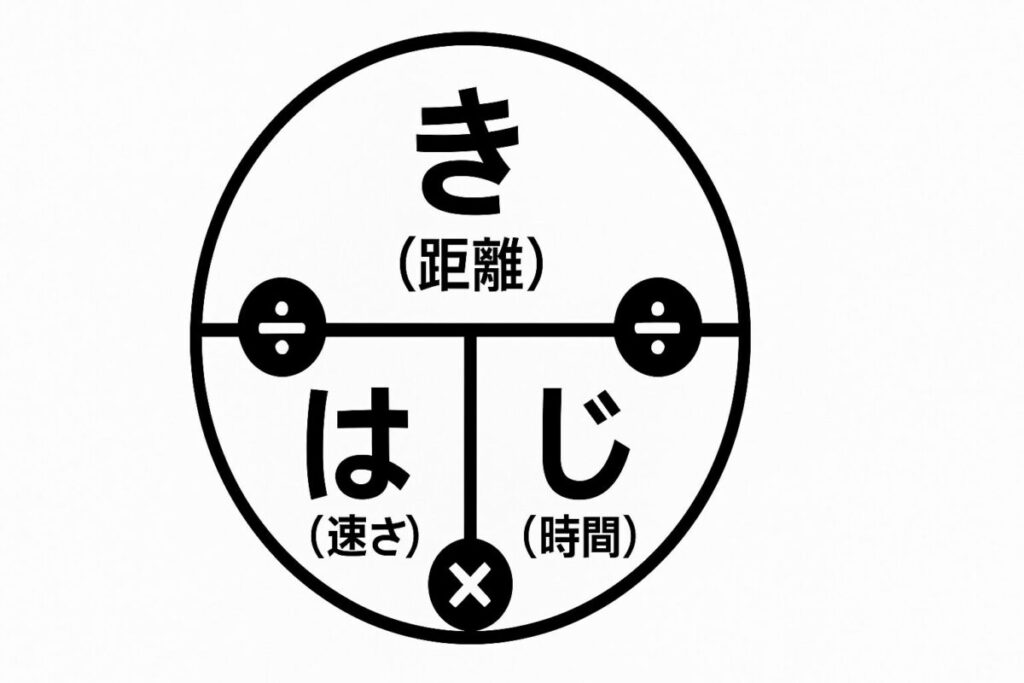
なぜこの図が便利かというと、求めたいものを指で隠すだけで、必要な「式」がパッとわかるから。
例えば、「距離」を求めたければ、上の「き」を指で隠します。すると、下に「は」と「じ」が横並びで残りますよね。これは「速さ × 時間」という掛け算を意味します。
「速さ」を求めたければ、左下の「は」を隠します。すると、「き」が上で「じ」が下、つまり「距離 ÷ 時間」という割り算の形が残ります。これは、「時間」ぶんの「距離」 という分数の形とまったく同じですね。
「時間」を求めたければ、右下の「じ」を隠します。すると、「き」が上で「は」が下、つまり「距離 ÷ 速さ」という割り算の形になります。これも、「速さ」ぶんの「距離」 という分数の形になっています。
どうでしょう?
たった一つの図を覚えておくだけで、3つの公式を丸暗記しなくて済むんです。これが「はじき計算」が長く使われている理由です。
3つの公式をマスター!「速さ」「時間」「距離」の求め方
「はじき計算」の図が便利なのはわかったけれど、実際にどうやって使うの?と思いますよね。
ここでは、3つのパターン(速さ・時間・距離)それぞれの式の作り方と、簡単な例題を見ていきましょう。
距離(道のり)を求める式とやり方
まずは「距離(き)」からです。
「距離」は、どれだけ進んだかを示す長さのこと。単位はkm(キロメートル)やm(メートル)がよく使われます。
図の上にある「き」を隠すと、「は」と「じ」が横に並びます。
これは掛け算を意味します。
公式:距離 = 速さ × 時間
とてもシンプルですね。
例えば、「時速50kmで走る車が2時間に進む距離は?」という問題を考えてみましょう。
- 速さ:時速50km
- 時間:2時間
これを式にあてはめると、
50(km/時) × 2(時間) = 100(km)
答えは100kmです。
文章問題で「距離は?」と聞かれたら、「速さと時間をかければいいんだな」と思い出してください。
速さを求める式とやり方
次に「速さ(は)」です。
「速さ」は、一定の時間でどれだけの距離を進めるかを示すものです。
時速(km/時)、分速(m/分)、秒速(m/秒)といった単位を使います。
図の左下にある「は」を隠してみましょう。
「き」が上に、「じ」が下に残りますね。これは割り算(分数)の形です。
公式:速さ = 距離 ÷ 時間
例えば、「150kmの距離を3時間で走った車の時速は?」という問題。
- 距離:150km
- 時間:3時間
これを式にあてはめます。
150(km) ÷ 3(時間) = 50(km/時)
答えは時速50kmとなります。
「速さは?」と聞かれたら、「距離を時間で割ればいい」と覚えましょう。
「1時間あたりにどれだけ進むか」を計算するのが速さ、と考えると分かりやすいかもしれません。
時間を求める式とやり方
最後に「時間(じ)」です。
「時間」は、ある距離を移動するのに、どれくらいかかったかを示します。
時間、分、秒が単位ですね。
図の右下にある「じ」を隠します。
「き」が上に、「は」が下に残りました。これも割り算です。
公式:時間 = 距離 ÷ 速さ
例題です。「時速60kmで走る車が、180kmの距離を進むのにかかる時間は?」
- 距離:180km
- 速さ:時速60km
式にあてはめてみましょう。
180(km) ÷ 60(km/時) = 3(時間)
答えは3時間です。
「時間は?」と聞かれたら、「距離を速さで割る」です。
速さが「1時間あたりに進む距離」なので、「全部の距離を、1時間あたりに進む距離で割れば、何時間かかったかがわかる」という理屈です。
はじき計算で間違えない!最大のコツは「単位」にあり
「はじき計算」の公式はカンタンですよね。
図さえ覚えてしまえば、掛け算か割り算をするだけ。
それなのに、なぜかテストで間違えてしまう…。
その最大の原因は、ほぼ「単位」にあります。
「はじき計算」を使いこなす最大のコツは、計算の前に「単位をそろえる」ことなんです。
なぜ単位をそろえる必要があるの?
例えば、こんな問題があったとします。
「時速60kmで走る車が、1200m進むのにかかる時間は何分ですか?」
この問題を、何も考えずに「はじき」にあてはめるとどうなるでしょう。
時間 = 距離 ÷ 速さ
時間 = 1200 ÷ 60 = 20
答えは20「分」…ではありませんよね。
どこが間違っているかわかりますか?
速さの単位は「時速(km/時)」、つまり「時間」と「km」が基準です。
それなのに、距離は「1200m」で計算してしまいました。
これでは、正しい答えが出るはずがありません。
「時速」と「m」という、違うルールの単位同士で計算してしまったのが失敗の原因です。
単位をそろえる「やり方」
では、どうすればよかったのでしょうか?
答えは、「計算の前に、どちらかの単位にそろえる」です。
この問題では、答えを「分」で聞かれています。
そのため、「速さ」の単位を「時速(km/時)」から「分速(m/分)」に直すのが良さそうです。
- 時速60km = 1時間(60分)で60km(60000m)進む
- 60000m ÷ 60分 = 1000m/分
つまり、「時速60km」は「分速1000m」と同じ速さだとわかりました。
これで単位がそろいましたね。
- 距離:1200m
- 速さ:分速1000m
もう一度、「時間 = 距離 ÷ 速さ」の式で計算してみましょう。
1200(m) ÷ 1000(m/分) = 1.2(分)
答えは1.2分です。
このように、「はじき計算」を使う前には、必ず「速さ」「時間」「距離」の単位がそろっているかを確認するクセをつけましょう。
時速なのに分で計算していないか?
kmなのにmで計算していないか?
この確認作業こそが、速さの問題をマスターする一番の近道であり、最大のコツですよ。
よくある疑問と応用テクニック
「はじき計算」の基本はマスターできましたね。
ここでは、さらによくある疑問や、単位変換をスムーズにするためのテクニックを紹介します。
「時速・分速・秒速」の変換がややこしい!
単位変換は、速さの計算で最もつまずきやすいポイントです。
特に「時速⇔分速⇔秒速」の変換は、パッと出てこないとなかなか大変。
基本は「1時間は60分」「1分は60秒」ということです。
| 変換元 | 変換先 | 計算方法 |
|---|---|---|
| 時速 | 分速 | ÷ 60 |
| 時速 | 秒速 | ÷ 3600 (60×60) |
| 分速 | 時速 | × 60 |
| 分速 | 秒速 | ÷ 60 |
| 秒速 | 分速 | × 60 |
| 秒速 | 時速 | × 3600 (60×60) |
この表を丸暗記するのも一つの手ですが、意味を理解するのが一番です。
「時速」は1時間(60分)で進む距離。
「分速」は1分間で進む距離。
当然、1分間で進む距離(分速)のほうが、1時間で進む距離(時速)よりも短くなりますよね。
だから、時速を分速に直すときは「÷ 60」する、と理屈で覚えてみましょう。
逆も同じです。
分速(1分あたり)を時速(1時間=60分あたり)に直すなら、60倍すればいいので「× 60」となります。
この理屈さえ押さえておけば、距離の「km」と「m」(1km = 1000m)の変換も落ち着いてできるはずです。
文章問題で何を聞かれているか見抜く方法は?
文章問題が苦手な人は、「結局、速さ・時間・距離のうち、どれを求めればいいの?」と混乱しがちです。
見抜くコツは、「問題文の最後」と「単位」に注目すること。
- 「〜の距離(道のり)は何kmですか?」→ 距離(き)を求める。単位はkm。
- 「〜の速さは時速何kmですか?」→ 速さ(は)を求める。単位は時速(km/時)。
- 「〜かかる時間は何分ですか?」→ 時間(じ)を求める。単位は分。
このように、問題文の最後が「?」で終わっている部分に、求めたいものと、答えるべき単位がはっきり書かれています。
ここを最初に確認してから、「はじき計算」の図のどれを隠すか(どの式を使うか)を決めましょう。
そして、問題文に書かれている他の情報(速さ、時間、距離)の単位が、答えるべき単位とそろっているかを確認します。
そろっていなければ、先に単位変換をしてから計算する。
この手順を守れば、文章問題も怖くありません。
まとめ
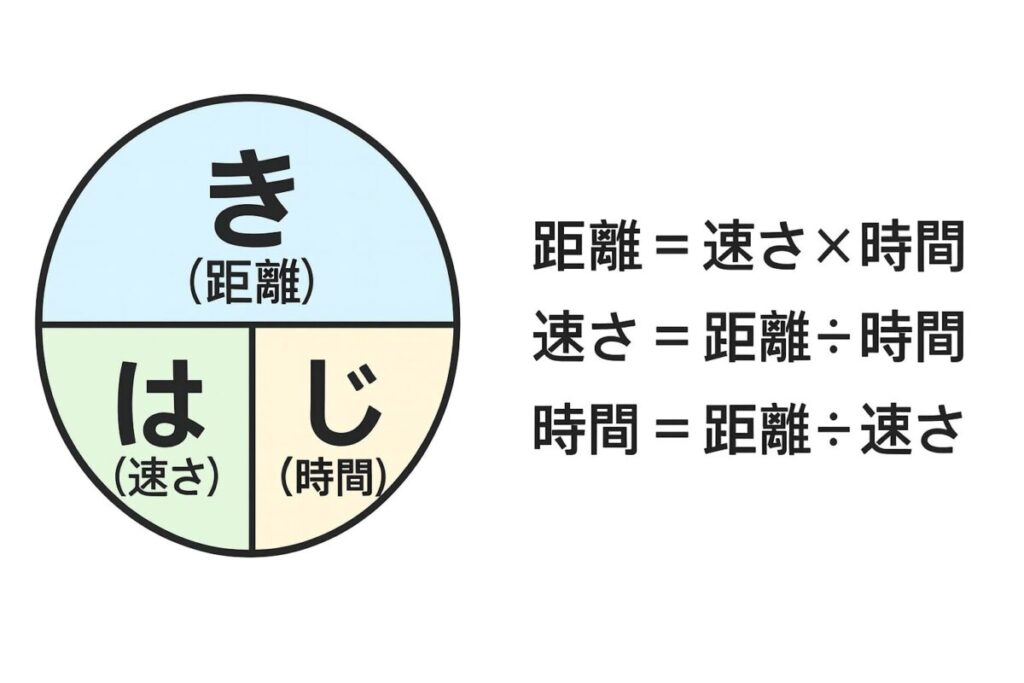
「はじき計算」は、速さ・時間・距離の関係をカンタンに思い出させてくれる便利なツールです。
- 求めたいものを隠せば、式が自然にわかる。
- 距離 = 速さ × 時間
- 速さ = 距離 ÷ 時間
- 時間 = 距離 ÷ 速さ
そして、何よりも大事なコツは「単位をそろえる」ことでした。
計算を始める前に、「時速」と「分」、「km」と「m」などが混在していないか、必ずチェックするクセをつけましょう。
この基本さえ押さえれば、算数や理科の文章問題もスラスラ解けるようになりますよ。